難易度の目安
| ☆の数 | 大雑把な意味 |
|---|---|
| ★☆☆☆☆ | 正答率が8割を超えている |
| ★★☆☆☆ | 解けないと不利 |
| ★★★☆☆ | 典型的な問題。医は必答 |
| ★★★★☆ | 差がついた問題 |
| ★★★★★ | 難しい |
大問1番(1)
ベクトルの典型的な問題。京大は、空間図形に関する問題が、2015年から2021年まで毎年出題されています。点が平面に関して対象である定義が書かれているので、それを使って解答するのが無難です。
ここでは平面の方程式を利用しましたが、正射影を用いた解答も同等に良いと思います。

大問1番(2)
僕はグループ分けの問題を解説するとき、「6人を①3つのグループA,B,Cに分ける②3つのグループA,B,Cに入れる③3つのグループに分ける」場合を例題に使います。この①のパターンと同じ、包除原理を利用する問題です。真ん中の項、2色を選ぶ場合の数に1色のみを選ぶ場合が含まれていることに気付かない事例が散見されます。(それを三つ目の項でキャンセリングしているのですね。)
意味を考えて解くより、事象を記号化して、包除原理を機械的に適用するのがベターです。コレも典型的な問題ゆえ、正答率は60%前後と思われます。

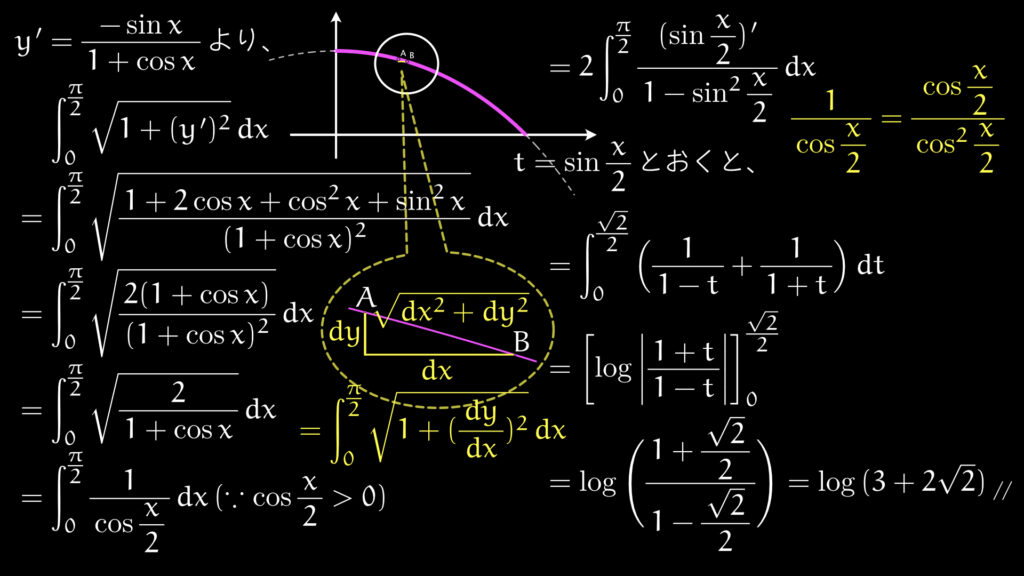
大問2番
考え方に難しいところは無くて、計算を正しく処理できるか否かの問題。計算を正しく処理できるというのは、複雑な式変形をミスなく行えるだけではなく、それよりも、いつも自分がしている、オーソドックスな計算に還元する能力も含みます。
三平方の定理を使う場面にて放物線の切り取る直線の長さで用いる計算。最大最小の問題かつ長さが正だから2乗した値に持ち込む計算。複二次式の適切な置換。どれもパターン化された計算であり、見慣れない式を力技で解くでは無く、オーソドックスな計算に帰着してください。

大問3番
場合分けの煩雑さにはウンザリします。複素数平面の知識で上手く解けないかと考えましたが、無限級数の定義に基づいた下記の周期6の場合分けが無難だと思います。周期12で分けてしまって、解き上げる能力も大切だと思うのですが、僕はどうにも、計算が一定量を超える解法は苦手です。
複素数平面の知識を用いた別解を、二枚目に掲載しています。こちらで解答する場合、極限の取り扱いに注意。答えを求めることは簡単ですが、極限に関して不正確な議論があると、簡単に0点です。

大問4番
典型問題。8割以上が完答したと思われます。大問2番にせよ、大問4番にせよ、京大の微積分は他大学に比べて平易な問題が多い傾向ですが、今年度は特に簡単だと感じました。
と思ったら、大問6番の(2)でやってくれました。
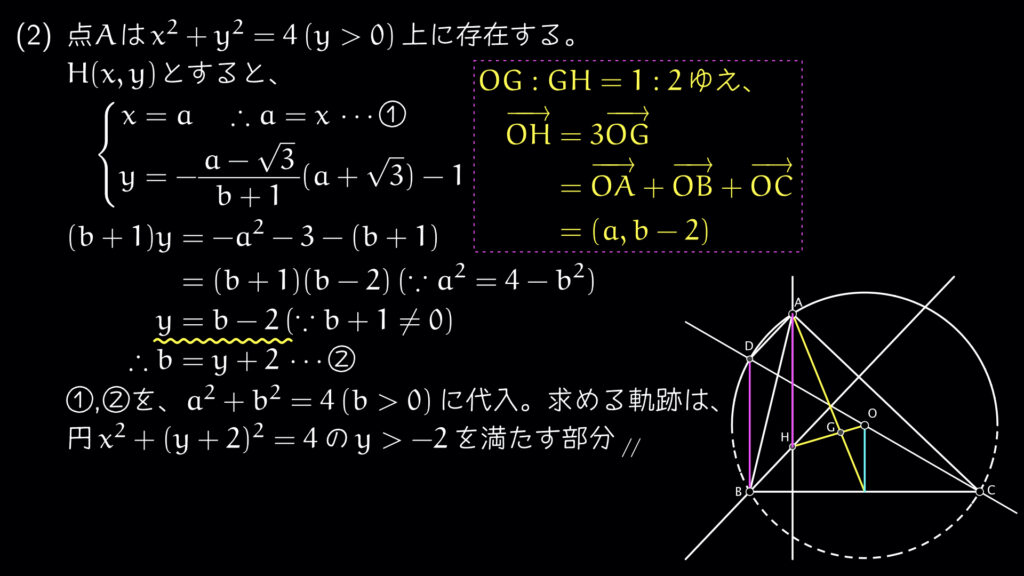
大問5番
円周角の定理と正弦定理(を使わなくとも、有名直角三角形だから分かりますが)から、外接円の半径2を求めて、2点B,Cから円の方程式が決まります=円の中心である外心の座標が分かります。外心の定義(=垂直二等分線の交点)と二等辺三角形の性質を用いて、線分BCの中点(0,-1)のy軸方向±1が必要条件だと分かります。
オイラー線(Euler’s line)を知っていれば、(2)でH(a,b-2)がすぐ求まります。当然、記述で使うのは非自明なのでバツですが、やや天下り的な途中の式変形の必然性に納得できると思います。

大問6番
結論より仮定がシンプルな形の命題を考えるのがセオリーなので、対偶をとりましょう。でも僕は最初しばらく元の命題のまま考えました。「○○が素数である」っていう仮定が、オイラーの定理(Euler’s theorem)とか使えそうな気がして、誘惑に駆られてつい……。
元の$$3^p-2^p>1$$を明らかとした解答に気をつけてください。当然バツです。

突然どうした?と思うぐらい、これまでと難易度にギャップを感じます。僕はグラフを書いて$$f(a)=af(1)$$の図形的意味((0,0),(1,f(1)),(a,f(a))が同一直線上に存在すること)を考察したら平均値の定理が浮かんで、条件式のままでは1とaが混在して使いづらいから変形して、その関数$$g(x)$$に先の定理を適用すれば良い結果が得られそうだと思って試しました。思いつけば後は簡単なところが、京大らしくて個人的に好きです。
平均値の定理を思いつく人は多かった一方、g(x)はほとんどが浮かばなかったようです。

