最近、初めて教育実習の指導教官になりました。自分が実習生だった頃の教育実習記録を読み返したら、ただひたすらに青くて顔から火が出る思いをしました。
2020年時点、自分なりの数学指導法を書き残しておこうと思いますが、2030年に見ても恥ずかしくないと良いなー。
問題
アガサ・クリスティは生涯に何冊の長編小説を書きましたか?どこかに、答えをメモして隠してください。
やる気を分類する話
効率の良い学習法のまえに、まずはやる気がないと意味ないので、やる気について書きます。
やる気にも種類があって、やる気の続かないものから順番に書きならべると、テンション、外発的モチベーション、内発的モチベーション、そして、内発的モチベーションが継続しているパッション。
この4つを、順番に説明します。
まず、テンションは上がりやすくて下がりやすいやる気です。円陣を組むとか、そんなんでも上がる。このやる気、持続しません。
外発的モチベーションは、成績のために勉強するとか、数学それ自体とは直接的に関わりのない目標です。即効性がある一方で、効果は一時的だし、さらには内発的モチベーションを阻害しかねません。
例えば、意味のない文字列を毎日3時間覚える。代わりに報酬が貰える。としましょう。何を貰えば、継続できますか?
お金が貰えるなら続くかもと思うかもしれませんが、何億円か貯まれば、もうお金は十分だから、辞めて楽しいことしたいなー、と僕なら思います。
結局、数学それ自体が意味のない苦痛である限り、せっせと新鮮な報酬を与え続ける必要があるんですね。
これが、外発的モチベーションの限界です。もし、文字列を覚えることが暗記術を身に付ける修行で、続けるほど暗記の天才になれるとかであれば、長く続くかも知れません。文字列を覚えること自体に意味のあるからです。
それが、内発的モチベーションです。
内発的モチベーションは、数学それ自体に何らかの意味を感じているものです。例えば因数分解。社会の役に立つって意味では素因数分解と暗号の話とかかなーと思うけれど、もっとシンプルでも良いわけです。
単純にできなかった因数分解が出来るようになる。不定方程式を解く際に使える。とかね。実際の内発的モチベーションを引き出すには、
何でも良いから意味を実感する。
ことが大切かなーと思います。
要するに、数学に対する内発的モチベーションを継続すること、つまり、パッションをもつことが理想です。
はじめから生徒達にパッションがあれば苦労しませんが、基本ないので、テンションや外発的モチベーションを足がかりに、内発的モチベーションを見つけてもらえるよう、見つけたら継続するようサポートしたいところ。
裁量とノームのある環境を作る話
読んで分かる通り、内発的モチベーションは強制されて生まれるものではありません。足がかりに強制力を使う場合はありますが、足がかりです。
カリスマ元塾講師の木下晴弘さんは、
「〇〇させる」という言葉は自然に反するものであることを理解したい。
と仰っています。めちゃ同感です。
「勉強させる」「相手を感動させる」環境は長続きしないでしょうね。
したがって、強制なく、内発的モチベーションを見つけてもらえるような環境がほしいわけです。僕が思うに、それは、自分に裁量のある環境です。
裁量のある環境とは、自分のしたいときに、したいことをする環境です。数学の勉強をしたいときにさせてあげる。ってことですね。
しかし実際にそんなことすると、なーんもやらなくなって、だったら意味がほとんど無くても良いから、強制的にやらせていた頃の方がヨカッタワ。なんて思い始めます。
それでも見守るというのは、本当に難しいですね。けれど、
プリントを一生懸命作ろうと、そもそもやる気のない人には資源の無駄。「せっかく作ったのにキーっ!!」って怒っても、無理に机に座らせても、出来ることは「見かけ」勉強させることだけです。
自分に出来ることは、プリントの質を高めるとかそれくらいです。
You can take a horse to the water, but you can’t make him drink.
(馬を水辺に連れて行くことはできても、水を飲ませることはできない)
これ、どこの言葉でしたっけ。忘れました。とにかく、裁量ある環境で、自ら勉強することで、有意義な学習になるんちゃうかなー、と思います。
ただ、これだけだと極端な話、「授業受けたくないし、今は喋りたいから私語します~」だって、本人の裁量といえば裁量ですし、何も言えない。
けどそれ、授業崩壊ですし。どうしよ。
よって、各人の裁量とは、規律=暗黙に了解されているルール上における裁量であって、当たり前のことはそもそも裁量できる範疇にないわけです。
先のカリスマ元塾講師木下さんはそれをノームと呼んでいます。例えば、裸で授業受ける人はいないし、「なんでダメなんだ!?俺はそうしたいんだ!!」とは思わないと思うんですよね。
「そりゃそうやろ」と思うのは、それが当たり前だからですね。けれど、何をもって当たり前とするかは、その集団の作る環境によると思います。
(実際、僕は出身が男子校でしたが、上裸で授業を受けている人いました)
というわけで、きちんとノームを作りましょう。ということです。でも、「○○しましょう(してはいけません)」ではダメです。破られるから。
多分どこでも、授業中は私語してはいけないし、集中しなさいってルールだと思うんですが、雑談やグループワークで私語は出るし、50分前後の授業をずっと全集中してる人いませんね。
実際は、「ずーっと集中できたら良いね☆」ぐらいの努力目標のわけで、それはノームとは呼べません。ルールとノームは違います。
ノームを形成するために、僕が気をつけていることが2つあります。
「集団が納得できるようなもので」
「徹底的に守る」
例えば、「こちらを向いて静かに聴いてください」と言って話すときは、徹底して、全員が黙って注視してくれていることを確認してから話します。
そんな感じで今のところ、一応は理想的な授業が出来ているわけですが、そもそも僕が教えてきた生徒はいわゆる育ちが良いタイプなので、イージーモードな環境でしか通じないかもですね。
軟葉高校とか行って、おんなじ教え方したらどうなるんだろう。
読んだら負け
アメリカの学術雑誌、Scienceに発表された論文の引用です。
パデュー大学のカーピック博士は、ワシントン大学の学生を集めました。そして、次の試験を行います。
① 4班に分ける
② 40個のスワヒリ語を目で見て覚える
③ 確認テストをする
(※↑各班の初期能力を揃えるため)
④ 各班、別の方法で覚える
一週間後、トップ班とドベ班の正答率は、2倍以上の開きがありました。トップ班は、単語を見て覚えたり、写経して覚えたりするインプット型ではなく、確認テストを繰り返すことで思い出そうとしたアウトプット班です。
このような学習方法を検索練習と呼びますが、具体的には
・フラッシュカード
・クイズ(発問)
・ペーパーテスト
・暗唱
などが検索練習。「思い出す」行為が大切なのです。
だから、数学が分からないとき、模範解答の読みに気を付けてください。模範解答を読みながら解答をノートに写すのではなく、模範解答を読んだら見ないでノートに再現してください。
大体どっかで詰まるので、そしたらまた読む。閉じる、書く、詰まる・・・を繰り返して、一週間後にあらためて解く。10日後でもいいけど。まあ、大体、それぐらい経ってもう一度解く。
それを何遍か繰り返すと、大体解けるようになります。
ところで、冒頭の問題の答えは66冊でした。自分の答えを見ずに、さっき自分は何冊だと推定したか思い出して、答え合わせしてください。
(答えあわせ)
先ほどの質問、答えの平均値は51冊でした。しかし、しばらく(数日間)経ってから答えを伝えて、「あのとき、貴方は何冊だと推定しましたか?」と聴くと、その平均値は63冊だったそうです。
記憶は、自分にとって都合の良い補正をされてしまうようです。
模範解答を読んだら、授業を聴いたら、分かった気になる。もしかして、後知恵バイアスがかかっているのかも知れない。と僕は思っています。
模範解答読んだら検索練習。授業聴いたら検索練習。オススメします。
頭を使わず計算し、頭を使って思考する
計算ミスが多発する人は、計算に頭を使っています。
計算に頭を使ってはいけません。母国語を話すように計算してください。例えば、今から晩ご飯のことを考えてください。何が食べたいでしょうか。考えながら、計算をしてください。
頭を使うべきは、対称性を見つけるなど、パターン認識です。
脳の延長領域として紙を使う
人が並列処理できる記憶は、限界があるそう。チャンクという固まりで、大体7チャンク前後が限界のようです。
このチャンク、決して7文字とか7単語と言うわけではなくて、1つの固まりと認識しているものが1チャンクです。例えば、
こぶた、fox、cat、きつね、
raccoon、ねこ、たぬき、pig
を覚えるには、整理して
こぶた(pig)、ねこ(cat)、
きつね(fox)、たぬき(raccoon)
さらに
こぶた → たぬき → きつね → ねこ
と考えれば、1つの固まりとして覚えることが容易です。
チャンクの説明はこんな感じですが、ちょっと横道に外れました。
僕が言いたかったことは、人間あんま覚えらんないよ、と言うことだったのですが…
計算ミスをする人は、頭でいくつも式変形をしてしまっているようです。例えば、次の平方完成をする際に
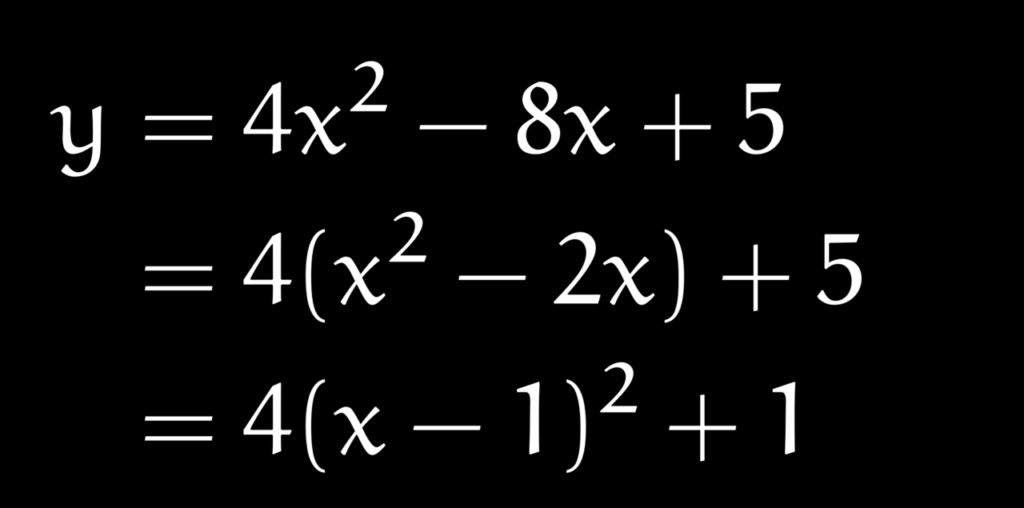
とすれば良いものを、慣れないうちから間の式を飛ばして
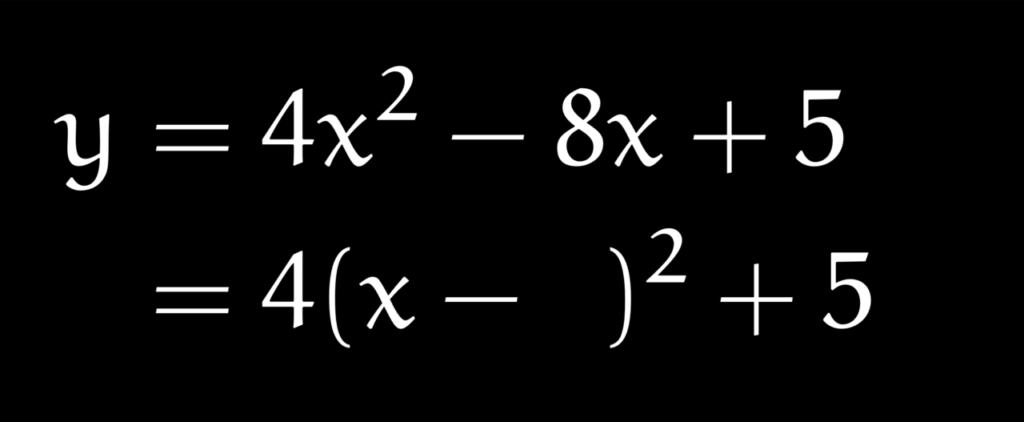
と書くから、計算をミスしてしまう傾向にあります。
紙と鉛筆は、脳の拡張領域だと思って広々デカデカ使うと良いです。
身体で解く
以前、数学する身体の書評を書きましたが、僕は数学は身体全体を使って考えた方がええんちゃうかと思っています。
パリ第11大学のノプス博士達は、足し算や引き算などの算術が、身体感覚に関係していることを発見しました。
眼球を左右に動かすときの「頭頂葉」の活動を記録して、次に、足し算か引き算をしてもらいました。足し算と引き算のどちらをしているか、博士達には分からないようになっていましたが、先の記録を利用して判断すると、高い確率でどちらの計算をしているか分かったそうです。
つまり、眼球を動かすときと足し算・引き算をしているときは、脳の同じ部位を同じように動かしていることになります。
脳を動かすために、身体を動かしている、ということです。
僕の経験則では、数学は書いたり喋ったりウロウロする方が効果的です。それに、運動はやる気を引き出すことも分かっています。ちなみに僕は数学が行き詰まったらその場でスクワットしてます。
そんなん筋トレっぽくて嫌だわ、と思うなら、お散歩はどうでしょう。
僕は朝が好きです。強いて言えば夏の朝が好きです。夏は夜らしいけど。夏に限らず、春夏秋冬いつでも、朝が一番好きです。外山滋比古さんが、『思考の整理学』という本で、「朝飯前」の意味について書かれています。(2020.07.30記。ご冥福をお祈りいたします)
(いまは、朝食前にも出来るほど簡単だ、の意で使われているのは、)朝の食事の前にするために、本来は、決して簡単でもなんでもないことが、さっさとできてしまい、いかにも簡単そうに見える。知らない人間が、それを朝飯前と読んだというのではあるまいか。どんなことでも、朝飯前にすれば、さっさと片付く、朝の頭はそれだけ能率がいい。
実に同感です。太陽の光がちょうど気持ち良く、紫外線がそうでもないし、お散歩にでも出てみようかしら、なんて気分になります。
道中にそれなりの自然でもあれば、いっそう素敵です。ただ自然もどきを歩くだけで、「グリーンエクササイズ」という立派なお名前がつきまして、ストレス軽減の効果があると、科学的に立証されています。
少し早歩きすると、なお運動になります。数学は決してインドア学問ではありません。
2020年時点、僕なりの数学勉強法でした。
